좋은 스키마와 나쁜 스키마
나쁜 스키마의 예시 1

3가지의 이상(anomaly)가 존재

- Update anomaly (갱신 이상) - chairman, building, budget 속성값이 deptName 값에 의존적이므로 학과명이 반복될 때 해당 속성값이 반복적으로 나오게 됨 / 갱신 시 모든 값을 동시에 갱신하여야 함
- Delete anomaly (삭제 이상) - 학과에서 제공하는 마지막 과목이 삭제되면 학과에 대한 다른 정보들도 함께 삭제되는 현상
- Insert anomaly (입력 이상) - 새로운 학과의 학과 정보를 입력하고자 하면 그 학과가 개설하는 과목이 없으면 입력할 수 없음 (주 키가 cID이므로)
나쁜 스키마의 예시 2

설계 목표
- 특정 관계 R이 좋은 형태인지 결정하는 것
- 관계 R이 좋은 형태가 아닌 경우, {R1, R2, ... Rn}처럼 관계의 집합 형태로 분해함
- 이 때, 각 관계는 좋은 형태여야 함 / 분해는 손실 없이 이루어져야 함
- 우리의 이론은 함수 종속성(functional dependencies)과 다치 종속성(multivalued dependencies)에 기반함
함수 종속성
- Legal Relation의 집합에 대한 제약
- 특정 속성 집합의 값이 다른 속성의 값을 유일하게 결정하는 것을 요구
- 함수 종속성은 키의 개념을 일반화한 것
함수 종속성의 정의

- R이 관계 스키마이고, α⊆R, β⊆R 인 경우
- 함수 종속성 α → β는 어떠한 유효한(legal) 관계에서든 그 관계에 속하는 두 튜플 t1과 t2가 속성 α에 대해
동의하면 t1과 t2는 속성 β에 대해서도 동의한다는 것을 의미 (t1[α] = t2[β] à t1[α] = t2[β]) - A 속성값이 같은 터플은 첫 번째와 두 번째 튜플이고, 첫 번째와 두 번째 튜플의 B 속성값이 동일하며, 그 외에는 동일한 속성값을 가지는 튜플이 없으므로, A는 B를 함수적으로 결정함 (A → B)
- 두 번째와 세 번째 튜플의 B 속성값이 같으나 A는 다르므로 B는 A를 함수적으로 결정하지 않음 (B /→ A)
함수 종속성과 키
- α → R를 만족한다면 스키마 R의 수퍼 키는 α임
- α → R를 만족하고 β ⊂ α 중에서 β → R을 만족하는 β가 없다면 α는 스키마 R의 후보 키임
- 후보 키는 모든 속성을 함수적으로 결정함
- Professor(pID, name, deptName, salary)에 대해 pID가 후보 키면 pID → name, deptName / pID → name 등이 결정
함수 종속성의 사용
- 주어진 함수 종속성 아래 관계 인스턴스가 유효(legal)한지 확인
- 관계 r이 주어진 함수 종속성 집합 F에 따라 유효하다면, 우리는 r이 F를 만족한다고 말함 - 유효한(legal) 관계 집합의 제약 명세
- R에 속하는 모든 유효한 관계가 함수 종속성 집합 F를 만족한다면, 우리는 F가 R에 성립한다고 말함 - 관계 스키마의 특정 인스턴스는 함수 종속성이 모든 유효한 인스턴스에 대해 성립하지 않아도 함수 종속성을 만족함
- 예를 들면 “professor”의 특정 인스턴스는 name → pID를 우연히 만족하는 경우가 있을 수 있음
함수 종속성 이론
어떤 함수 종속성이 주어진 함수 종속성의 집합으로부터 논리적으로 유도되는지 알려주는 형식적 이론
Trivial (무의미) 함수 종속성
- 함수 종속성이 모든 관계 인스턴스에 대해 만족하면 무의미(trivial)하다고 함
- 일반적으로 β ⊆ α 인 경우, α → β는 무의미하다고 함
- ID name → ID : ID는 자기 자신에 대해 항상 종속되기 때문에 무의미함
- name → name : name은 자기 자신에 대해 항상 종속되기 때문에 무의미함
함수 종속성의 폐포 (Closure of a set of functional dependencies)
- 함수 종속성 집합 F가 주어졌을 때, F에 의해 논리적으로 유도되는 다른 함수 종속성이 있음
- A → B, B → C이면 A → C가 성립
- F에 의해 논리적으로 유도된 모든 함수 종속성을 F의 폐포(closure)라고 하며 F+라고 함 (F+은 F의 Superset임)
암스트롱 공리 Armstrong’s Axioms
암스트롱 공리를 이용하여 모든 F+를 찾을 수 있음

예제 : R = (A, B, C, G, H, I) / F = {A → B, A → C, CG → H, CG → I, B → H}
- F로부터 유도할 수 있는 몇몇 함수 종속성
- A → H : A → B, B → H
- AG → I : CG → I, AG → CG (A → C)
- CG → HI : CG → I가 CG → CGI로 부가, CG → H가 CGI → HI로 부가, 이후 이행성 이용
- A → BC : A → B, A → C
암스트롱 공리는 sound하고 complete함
- sound(건전성) : 실제로 유효한 공리만 생성
- complete(완전성) : 모든 유효한 함수 종속성을 공리를 사용하여 생성 가능
3가지의 공리만을 이용하여 어떠한 함수 종속성이라도 유도해낼 수 있음
추가 추론 규칙

함수 종속성 폐포를 구하는 방법 (F+를 계산하는 방법)
- F+ = F (F+를 F로 초기화)
- F+의 각 함수 종속성 f에 대해 반복
- 재귀성(reflexivity) 룰과 부가성(augmentation) 룰을 적용 / 결과적인 함수 종속성을 F+에 추가 - F+의 각 함수 종속성 쌍인 f1과 f2에 대해 반복
- f1과 f2가 이행성(transitivity)을 통해 결합할 수 있다면 그 결과를 F+에 추가 / F+가 변경되지 않을 때까지 반복 - 위 과정은 F+를 계산하는 이론적 방법 (실제로는 사용하지 않고 다른 대안을 사용)
속성 집합의 폐포 (Closure of Attribute Sets)

속성 집합의 폐포 예시

AG가 후보 키인가? -> 먼저 AG가 수퍼 키인지 확인, AG → ABCGHI (모든 속성) 이므로 수퍼 키가 맞음 -> AG의 부분 집합이 수퍼 키인지 확인, A → ABCH, G → G 이므로 수퍼 키가 아님 -> AG는 후보 키가 맞음
속성 폐포의 사용

Canonical Cover (정규 커버)
- 함수 종속성 집합에는 다른 것들로 유도할 수 있는 중복된 종속성이 있을 수 있음
- { A → B, B → C, A → C }에서 A → C는 중복 - 함수 종속성의 일부분이 중복될 수 있음
- {A → B, B → C, A → CD}는 {A → B, B → C, A → D}로 단순화될 수 있음
- {A → B, B → C, AC → D}는 {A → B, B → C, A → D}로 단순화될 수 있음 - 우리는 중복된 종속성이나 종속성의 중복된 부분이 없는 F+와 동등한 함수 종속성 F 집합을 원함
- 함수 종속성 집합 F에 대한 Canonical Cover Fc는 다음 조건을 만족
- F+ = Fc+
- Fc에 있는 어떠한 함수 종속성도 불필요한 속성을 포함하지 않음
- Fc의 각 함수 종속성의 왼쪽 부분은 고유함
F의 Canonical Cover 계산 방법

Canonical Cover 예제

Normal Forms 정규형
First Normal Form (1NF) 제1정규형
도메인의 요소들이 나뉘질 수 없으면 도메인이 원자적(atomic)이라고 함
non-atomic 도메인의 예 : 집합, 리스트, 백(bags), 복합 속성 등
도메인의 모든 속성이 원자값이면 관계형 스키마 R은 제1정규형에 속함 (관계의 형식적인 정의)
다양한 함수 종속성

Second Normal Form (2NF) 제2정규형
만약 관계 스키마 R이 제1정규형에 속하고 R의 모든 비주요 속성 A가 R의 모든 후보 키로부터 완전 함수 종속이라면 제2정규형이라고 함

제1정규형, 제2정규형 예제

Third Normal Form (3NF) 제3정규형
제2정규형 중에서 비주요 속성이 모든 후보 키에 이행적으로 의존적이 아니면 제3정규형임

제2정규형, 제3정규형 예제

Boyce/Codd Normal Form (BCNF)

제3정규형, BCNF 예제

속성이 2개인 테이블은 모두 BCNF임
- R(A, B) 스키마와 가능한 모든 함수적 종속성을 고려하면 4가지 경우가 나옴
- 의미 있는 함수 종속성이 없는 경우 / (A, B)가 후보 키가 됨 -> BCNF
- A → B가 성립하고 B → A는 성립하지 않는 경우 / A가 후보 키이므로 BCNF에 속함
- B → A가 성립하고 A → B는 성립하지 않는 경우 / B가 후보 키이므로 BCNF에 속함
- A → B와 B → A가 모두 성립하는 경우 / A와 B가 둘 다 후보 키이므로 BCNF에 속함
정규형 관계도
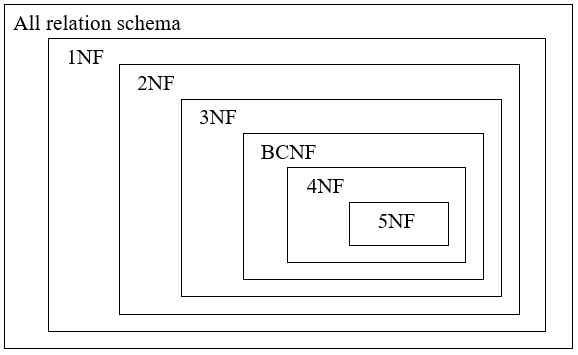
가능한 관계형 스키마 중에서 일부가 제1정규형이고,
제1정규형 중에 일부가 제2정규형이며,
제2정규형 중의 일부가 제3정규형이며,
제3정규형 중의 일부가 BCNF 정규형이 됨
실세계에서는 제3정규형과 BCNF 정규형을 사용하는 것을 권장


Decomposition and Design 분해 및 설계
정규화 목표
- R은 관계형 스키마, F는 함수 종속성의 집합이라고 가정
- 주어진 R이 좋은 형태의 스키마인지 결정
- 만약 좋은 스키마가 아니라면 분해를 통해서 관계형 스키마의 집합으로 만듦 {R1, R2, ... Rn}
- 이 때, 각 관계 스키마는 좋은 스키마여야 함
- 분해는 손실이 없는 조인 분해를 이용
- 함수 종속성을 보존하는 분해면 더 좋음
무손실 조인 분해 예제 (Lossless-Join Decomposition)

분해된 두 테이블의 자연 조인 연산이 원래 테이블과 동일하면 무손실 조인 분해임
R이 R1과 R2로 무손실 조인 분해되면, F+의 최소 하나의 종속성이 다음과 같아야 함
R1 ∩ R2 → R1 or R1 ∩ R2 → R2 / 분해된 테이블 중 하나에서 해당 속성을 모두 결정해야 함
위 조건은 분해가 무손실 조인 분해가 되기 위한 충분조건
만약 모든 제약이 함수 종속성이면 필요조건이 되기도 함
함수 종속성 보존
(F1 ∪ F2 ∪ ... ∪ Fn)+ = F+ 이면 분해는 종속성 보존임 (Fi는 Ri에 속하는 속성만 포함하는 종속성 집합)
만약 종속성이 보존되지 않으면 함수 종속성 위반을 체크하기 위해 조인 계산이 필요하며 이는 비용이 많이 듦
함수 종속성 보존 테스트

분해(Decomposition) 예제

BCNF 테스트
간단한 테스트 : 관계형 스키마 R이 BCNF인지 확인하려면 F+의 모든 종속성을 확인하는 것보다 주어진 F 집합의 종속성만 확인하면 충분함
- F의 종속성이 BCNF와 위반을 발생시키지 않는다면 F+의 종속성도 위반을 발생시키지 않을 것임
이 간단한 테스트는 R이 R1, R2, ... Rn으로 분해되어 있다면 작동하지 않음
- R = (A, B, C, D, E) / F = {A → B, BC → D} 의 경우
- R1 = (A, B), R2 = (A, C, D, E) / F의 어떤 종속성도 (A, C, D, E)에서 파생된 속성만을 포함하지 않음
- 하지만 AC → D가 F+에 속함, 그러므로 R2는 BCNF가 아님
분해 시의 BCNF 테스트
R의 분해인 Ri이 BCNF에 속하는지 확인하는 방법
Ri에 대한 F를 Ri의 속성만 포함하도록 제한한 경우의 BCNF 테스트를 수행
(즉, Ri에서 파생된 속성만을 포함하는 F+의 모든 함수적 종속성에 대해 BCNF 테스트를 수행)
또는 R에 적용되는 원래의 종속성 집합 F를 사용하고 다음과 같은 테스트를 수행

BCNF 분해 예제
- R = (A, B, C) / F = {A → B, B → C}
- 후보 키 = {A}
- R은 BCNF가 아님 (B → C에서 B가 수퍼 키가 아니기 때문)
- 분해 => R1 = (B, C) / R2 = (A, B)
BCNF와 함수 종속성 보존
- 함수 종속성을 포함한 제약은 단일 관계에 적용되는 것이 아니면 확인하기 어려움
- 각각의 분해된 관계에 대해 개별적으로 종속성이 유지되는 것이 확인되면 해당 분해는 종속성 보존이라고 함
- BCNF와 종속성 보존을 동시에 달성하는 것이 항상 가능하지 않으므로 더 약한 정규형인 제3정규형을 고려
- R = (J, K, L) / F = {JK → L, L → K}
- 후보 키 : JK and JL
- R은 BCNF가 아님 (L → K에서 L이 수퍼 키가 아니기 때문)
- R의 분해로는 JK → L을 확인하는 것이 불가능(조인해야 가능함) -> 함수 종속성은 보존되지 않는 분해임
제3정규형의 사용 동기(Motivation)
- BCNF가 종속성 보존이 아니며 업데이트에 관한 함수 종속성 위반 체크가 중요한 경우가 있음
- 제3정규형이라는 더 약한 정규형을 사용
- 어느 정도의 중복을 허용
- 함수 종속성을 조인 계산 없이 개별 관계에서 확인 가능
- 제3정규형으로의 무손실 조인 분해와 함수 종속성 보존 분해는 항상 가능
제3정규형에서의 중복
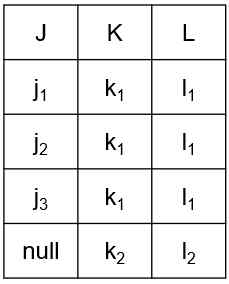
- R = (J, K, L) / F = {JK → L, L → K} / 후보 키 : JK and JL / R = 3NF
- JK → L : JK가 수퍼 키임 / L → K : K가 주요 속성임
- 일부 중복이 있음
- 정보의 반복 (l1과 k1의 경우)
- null 값을 사용해야 함 (J에 해당하는 값이 없는 관계 l2, k2를 나타내기 위해)
제3정규형 테스트
F의 함수 종속성만 확인하면 됨 (F+의 모든 함수 종속성을 확인할 필요 없음)

BCNF와 3NF의 비교
- 항상 한 관계를 3NF에 속하는 여러 관계로 분해할 수 있음
- 분해는 손실이 없음 / 종속성이 보존
- 항상 한 관계를 BCNF에 속하는 여러 관계로 분해할 수 있음
- 분해는 손실이 없음 / 종속성을 보존하는 것이 항상 가능하지 않을 수 있음
데이터베이스 설계
- 관계형 데이터베이스 설계의 목적
- BCNF 사용 / 무손실 조인 분해 / 함수 종속성 보존 - 이를 달성할 수 없다면 다음 중 하나를 수용
- 종속성 보존의 부재 / 3NF 사용으로 인한 중복 - SQL은 기본/후보 키를 선언하는 것 외에는 함수적 종속성을 직접 지정하는 직접적인 방법을 제공하지 않음
- 함수적 종속성을 지정하려면 현재 어떤 상용 데이터베이스 시스템도 지원하지 않는 assertion을 사용해야 함 - 스키마 R이 주어졌다고 가정
- ER 다이어그램이 테이블의 집합으로 변환될 때, R은 생성될 수 있음
- R은 모든 관심 속성을 포함하는 단일 관계일 수 있음 (universal relation이라고 함)
- 정규화는 R을 더 작은 관계로 분해
- R은 어떤 임의의 관계 설계의 결과일 수 있으며 우리는 이를 테스트하거나 정규형으로 변환할 수 있음
- ER 다이어그램이 모든 개체를 올바르게 식별하고 신중하게 설계된 경우,
ER 다이어그램에서 생성된 테이블은 추가적인 정규화가 필요하지 않아야 함 - 하지만 실제 불완전한 설계에선, 개체의 non-key 속성에서 개체의 다른 속성으로의 함수 종속성이 생길 수 있음
- 예 : departmentName과 building 속성을 가진 employee 개체와 "departmentName → building" 함수 종속성
-> 좋은 설계는 department를 별도의 개체로 만들어야 함 - 관계 집합의 non-key 속성에서의 함수 종속성은 가능하지만 드문 경우임 (대부분의 관계는 이진 관계이기 때문)
성능을 위한 역정규화 (Denormalization)
성능을 위해서 비정규화된 스키마를 사용할 수도 있음
"course"와 "takes"의 속성을 모두 포함하는 비정규화된 관계를 사용하여 "sID"와 함께 "course title"을 표시하는 경우 "course"와 조인이 필요함

Multivalued Dependencies 다치 종속성
다치 종속성 예제
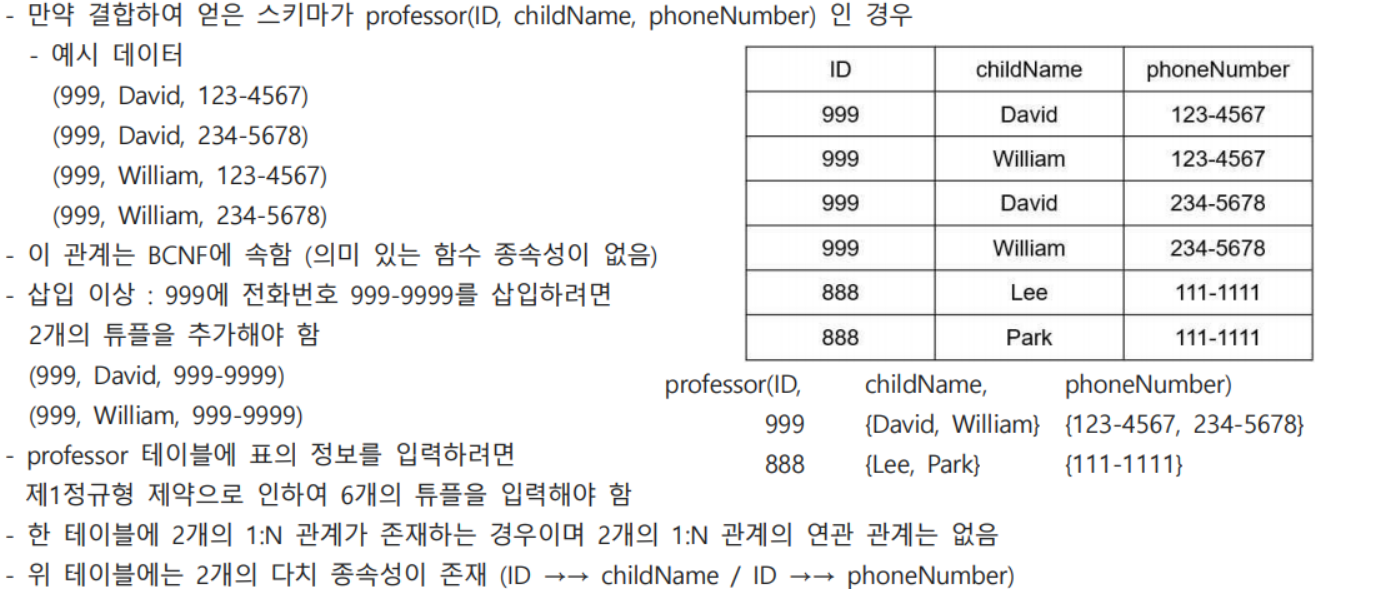
교수에 대하여 아이들의 이름과 전화번호를 기록한다고 가정
- profChild(ID, childName)
- profPhone(ID, phoneNumber)
다치 종속성의 정의
첫 번째 정의
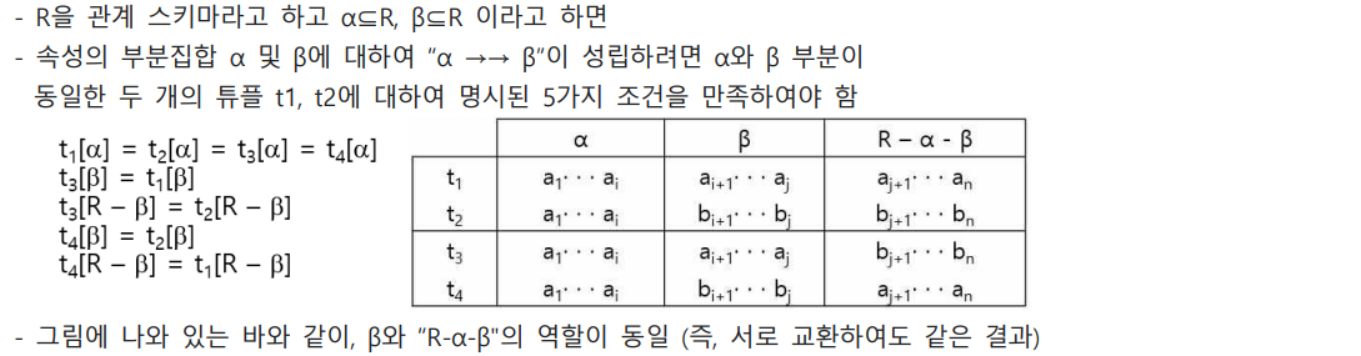
두 번째 정의

다치 종속성의 사용
보통 2가지 방법으로 다치 종속성을 사용
- 주어진 일련의 기능적 및 다중값 종속성 하에서 관계가 유효한지(legal) 확인하는 데 사용 (주어진 함수 종속성과 다치 종속성이 주어진 테이블 인스턴스에 만족하는지를 확인하여 테이블 인스턴스의 유효성 여부를 결정하는 데 사용)
- 유효한(legal) 관계 집합에 제약을 지정하는 데 사용 (주어진 기능적 및 다중값 종속성을 만족하는 관계에만 관심을 가짐)
다치 종속성 이론

Fourth Normal Form (4NF) 제4정규형

제4정규형 예제

다치 종속성 분해 예제

기타 정규형
- 조인 종속성은 다치 종속성을 일반화함
- 프로젝트 조인 정규형(PJNF : project-join normal form) 또는 제5정규형(fifth normal form)이라고 함
- 더 일반적인 제약의 클래스는 domain-key 정규형이라고 불리는 정규형으로 이어짐
- 이러한 일반화 제약은 이해하기 어렵고 의미론적 추론에 사용할 완전한 규칙 세트가 존재하지 않아서 거의 사용되지 않음
'Database [DB]' 카테고리의 다른 글
| [DB] 07. Entity-Relationship Data Model (3) | 2024.01.09 |
|---|---|
| [DB] 06. Application Development (1) | 2024.01.08 |
| [DB] 05. Major Functionalities of Database Systems (3) | 2024.01.08 |
| [DB] 04. SQL 2 (0) | 2024.01.07 |
| [DB] 03. SQL 1 (1) | 2024.01.07 |



