다차원 데이터
- 전통적인 1차원 데이터 레코드가 아니라 CAD나 지리정보 시스템에서의 선, 면, 위치와 같은 데이터
- 다차원 데이터를 나타내는 (x, y), (x, y, z)는 차원 당 하나의 값
- 다차원 데이터는 단일 키 화일 구조로 처리 불가능
- 다차원 데이터의 접근을 위해서는 다차원 인덱스 구조가 필요하다.
다차원 공간 화일
여러 개의 필드(차원)를 동시에 키로 사용하는 화일
다차원 인덱스 기법
- PAM : 다차원 점 데이터를 공간에 저장, 검색하는 점 접근 방법
Point Access Method : k-d 트리, k-d-B 트리, 격자 화일 - SAM : 선, 면, 다각형, 다면체 같은 다차원 공간 데이터를 저장, 접근할 수 있는 공간 접근 방법
Spatial Access Method : R-트리, R*-트리, R+-트리
k-d 트리
기본 개념
- k 차원의 점 데이터를 인덱스하는 구조
- 이원 탐색 트리를 다차원 공간으로 확장한 것 (= 다차원 이원 탐색 트리)
- 기본 구조와 알고리즘은 이원 탐색 트리와 유사 (작거나 같으면 왼쪽, 크면 오른쪽)
- 트리의 레벨을 내려가면서 차원의 필드 값을 차례로 번갈아 가며 비교
특징
- 메인 메모리에서 동작하는 인덱스 구조
- 소규모 다차원 점 데이터 인덱싱에 적합 (PAM)
- 균형 트리가 아님


k-d-B 트리
k-d 트리와 B-트리의 특성 결합
- 디스크 기반으로 다차원 점 데이터를 효율적으로 검색, 저장하기 위한 구조
- 디스크 페이지 크기의 노드들로 구성된 다원 탐색 트리 / 균형 트리 (루트에서 리프 노드까지의 탐색 경로 길이가 모두 동일)




격자 화일 (Grid file)
기본 개념
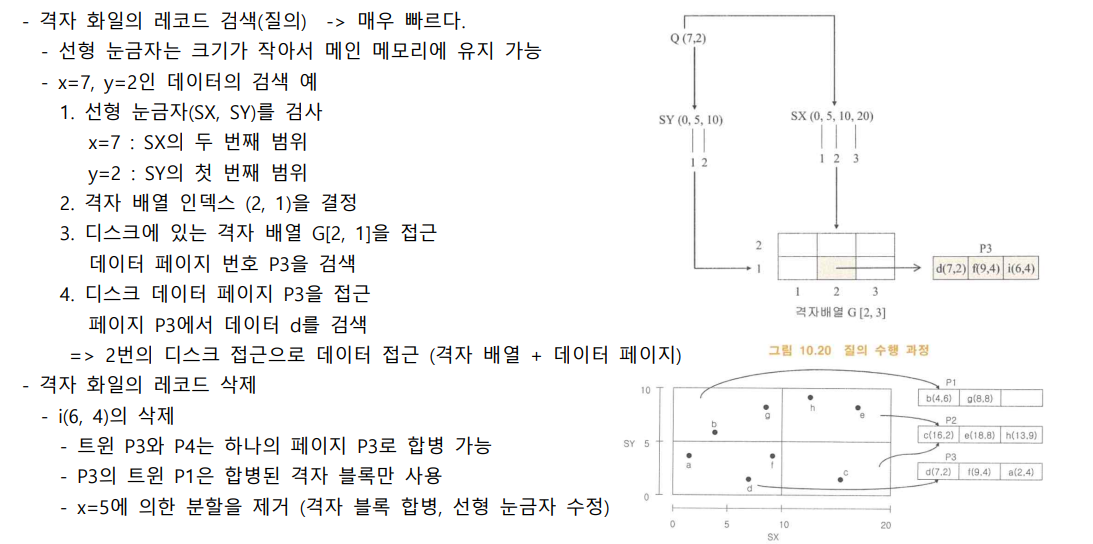
- 공간상의 점 데이터를 저장하는 다차원 인덱스 구조
- 전체 공간을 격자로 분할하여 격자 단위로 데이터를 저장
- 격자의 크기는 데이터의 삽입에 따라 분할되어 작은 격자로 변환
특징
- 디스크 기반 : 대용량의 다차원 데이터를 처리
- 해싱 기반 : 일반적으로 두 번의 디스크 접근으로 데이터를 검색


사분 트리 (Quadtree)
기본 개념
- 공간을 반복적으로 분해하는 성질을 가진 계층적 자료 구조를 표현하는데 사용
사분 트리의 구분
- 표현하고자 하는 데이터의 유형
- 공간 분해 방법
- 해상도 : 분해 레벨 정도를 고정 또는 가변
표현 대상 데이터
- 점, 영역, 곡선, 표면, 볼륨 데이터
- 개체의 경계를 표현하는 경우(곡선, 표면)와 개체의 내부를 표현하는 경우(영역, 볼륨)에 따라 상이한 자료구조를 사용
공간 분해 방법
- 이미지 공간 계층 : 각 레벨마다 공간을 일정 크기의 동일한 소공간으로 분해
- 객체 공간 계층 : 입력 데이터 값에 따라 가변적 크기의 공간으로 분해
가장 많이 사용되는 사분 트리
- 영역 사분 트리 : 2차원의 영역 데이터를 표현
- 점 사분 트리 : 다차원 점 데이터를 표현

영역 사분 트리의 루트 노드는 이진 배열 전체에 대응한다.
한 노드의 자식 노드들은 그 부모 노드가 표현하는 영역의 한 사분면을 표현 (NW, NE, SW, SE로 레이블을 붙임)
리프 노드는 더 이상 분할이 필요 없는 블록에 대응한다.
리프 노드는 대응되는 블록이 표현된 영역 외부/내부에 있느냐에 따라 2가지 종류로 나뉜다.
- 흑색 노드 : 블록이 완전히 영역의 내부에 포함되어있다. 1로 표현된 서브 사분면
- 백색 노드 : 블록이 완전히 영역의 외부에 포함되어있다. 0으로 표현된 서브 사분면
- 회색 노드 : 리프 노드가 아닌 노드 (0, 1로 표현된 블록을 모두 포함한다.)

점 사분 트리의 검색
- 탐색 공간을 좁혀 나가는 기법 : 한 레벨 내려가면 탐색 공간은 1/4로 감소
- 리프 노드가 가리키는 버킷에서 원하는 데이터를 검사
- 예시 : (95, 8)에 위치한 도시를 검색하라 -> 대전의 SE, 진주의 SE, 부산의 NE에 속하므로 버킷 23을 조사 - 범위 탐색이나 근접 탐색에도 적용
- 예 : (83, 10)에서 거리 8이내의 모든 도시 검색 : 대전의 SE를 검색하고 진주의 NE와 SE만 검색하면 됨
점 사분 트리의 삭제
- 삭제는 복잡 : 삭제할 노드를 루트로 하는 서브 트리에 있는 모든 노드들이 재삽입되어야 한다.
- 이상적인 삭제 방법 : 삭제할 노드 A를 어떤 노드 B로 대치한 후 삭제
- -> 이때, 노드 B는 노드 A를 루트로 하는 서브 트리의 노드들이 속한 사분면에 영향을 주지 않아야 한다.
- -> 이런 B가 존재하지 않을 경우, 가장 근접한 것으로 대체 후 영역에 존재하는 점 데이터를 재삽입한다.
R-트리
B-트리를 다차원으로 확장시킨 완전 균형 트리
점, 선, 면, 도형 등 다양한 다차원 공간 데이터 객체를 저장하고 검색하기 위한 다차원 인덱스 구조 (SAM)
모양이 불규칙한 공간 데이터 객체를 저장하기 위하여 객체의 최소 경계 사각형 MBR을 구하여 인덱스 엔트리로 저장
MBR : Minimum Bounding Rectangle / 대신에 MBB(Minimum Bounding Box)로 표현하기도 한다.

R-트리의 개념
- B-트리를 다차원 구조로 확장
- 디스크 페이지 단위로 데이터를 저장, 검색 가능 -> 대용량 데이터에 대한 인덱스 구조로 적당
- 인덱스 구조는 B-트리와 같이 높이 균형 트리
- 리프 노드의 엔트리는 객체 MBR과 이 객체가 저장된 주소(포인터)로 구성
- 중간 노드의 엔트리는 자식 노드의 모든 MBR을 포함하는 보다 큰 MBR과 자식 노드에 대한 포인터로 구성
R-트리의 특성 (M : 한 노드가 저장 가능한 최대 엔트리 수 / m : 최소 엔트리 수 (m≤M/2) )
- 루트 노드가 아닌 노드는 최소 m, 최대 M개의 인덱스 엔트리와 자식 포인터를 포함한다.
- 루트 노드는 리프가 아닌 이상 최소 2개의 자식 노드를 갖는다.
- 모든 리프 노드는 최소 m, 최대 M개의 인덱스 엔트리를 포함한다.
- 리프 노드에 있는 각 인덱스 엔트리는 객체 데이터를 실제 공간적으로 포함하고 있는 MBR과 이 공간 객체가 저장된 페이지 주소를 포함한다.
- 완전 균형 트리이다. 즉 모든 리프 노드는 같은 레벨에 있다.
- 점 데이터를 주로 처리하는 k-d-B 트리는 데이터 자체를 분할하는 것이 아닌 영역을 분할하기 때문에 중간 노드들의 영역이 중첩될 수 없다.
- R-트리는 데이터 객체들을 분할하고 이들을 포함하는 영역을 MBR로 표현하는 것이기 때문에 MBR이 서로 겹칠 수 있고 또 전체 영역 중에는 어떤 MBR에도 포함되지 않는 영역이 있을 수 있다.
- 따라서 R-트리는 중간 노드들이 포함하는 MBR이 중첩될 수 있기 때문에 임의의 크기의 객체를 분할 저장하기 쉽다.







R-트리의 변형 트리 : 성능 향상이나 다양한 응용 지원을 위한 변형 트리
- R+트리 : R-트리에서 노드 간의 중첩 영역을 없앰, k-d-B 트리의 특징을 접목
- R*-트리 : R-트리의 삽입, 삭제 알고리즘을 개선
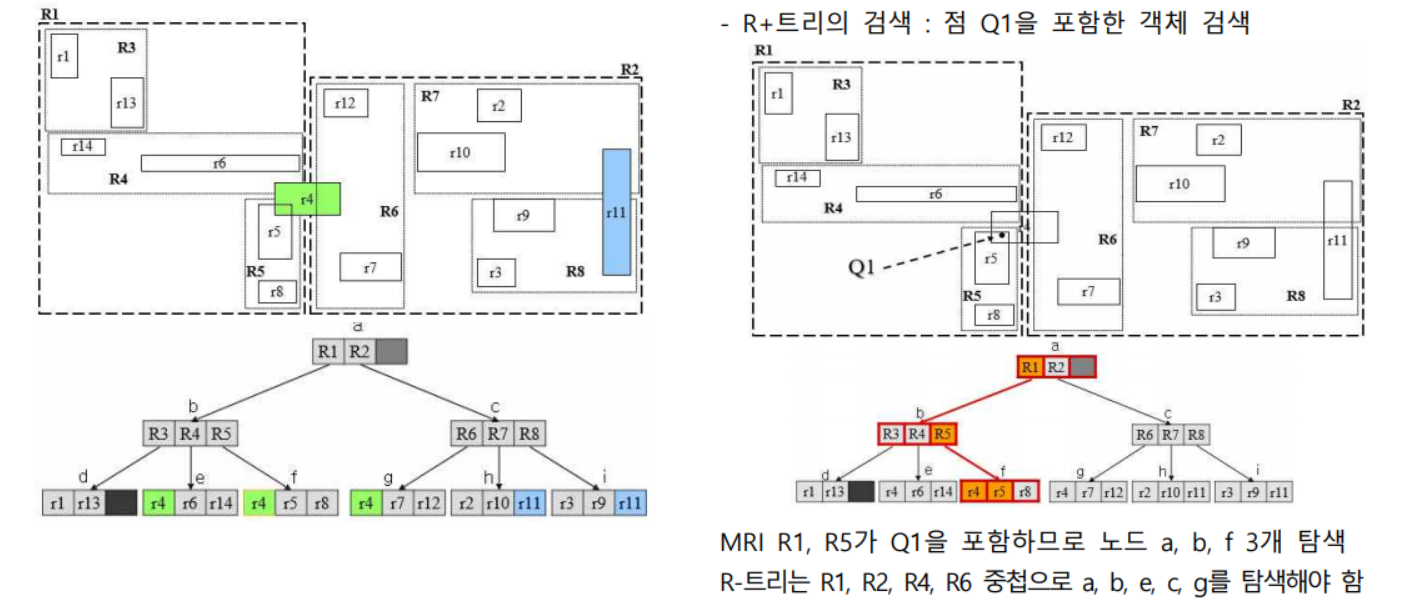
R+트리
여러 MBR과 중첩되는 데이터는 여러 노드에 중복 저장
- 데이터가 분할되도록 MBR을 설정할 수 있음
- 중간 노드 MBR들은 중첩이 필요 없다.
- 데이터를 저장할 때는 데이터 일부가 아니라 데이터 객체 전체를 저장한다.
R-트리와의 차이점
- R+트리의 노드는 적어도 1/2이상의 엔트리가 채워진다는 것을 보장하지 않음
- R+트리의 중간 노드들은 MBR은 중첩되지 않음
- R+트리의 데이터 객체는 분할 가능, 이 경우 데이터 객체 전체가 둘 이상의 리프 노드에 중복 저장된다.
R+트리의 삽입과 삭제는 R-트리보다 복잡
- 하나의 데이터 객체가 여러 리프 노드에 중복될 수 있기 때문
R+트리의 삽입
- 데이터 객체를 삽입해야 될 모든 리프 노드를 찾음
- 삽입하는 데이터 객체의 MBR이 중간 노드의 MBR과 중첩되면 중첩되는 MBR을 통하는 경로에 도달하는 모든 리프 노드에 중복 저장
- 삽입하는 데이터 객체의 MBR이 기존의 중간 노드 MBR에 포함되지 않으면 기존 MBR을 조정
- 리프 노드에 삽입할 때 만원이면 노드를 분할
R+트리의 삭제
- 해당 객체가 하나 이상의 리프 노드에 저장될 수 있으므로
해당하는 모든 리프 노드에서 해당 객체를 삭제해야 한다. - 삭제가 많이 발생한 뒤에는 공간 활용도가 매우 나빠질 수 있다.
- 이런 경우, 성능을 고려하여 주기적으로 서브 트리들을 재구성해야 한다.
R+트리의 장점
- MBR이 중첩될 때의 문제점을 해결
- 불필요한 노드 탐색을 줄임
R+트리의 단점
- 노드의 분할이 상위 노드뿐만 아니라 하위 노드로도 파급될 수 있음
- 즉, 중간 노드의 분할은 하위 노드 전체를 분할하게 할 수 있음 -> 노드의 공간 활용도가 나빠짐
- 리프 노드에 중복되어 저장되는 데이터의 수는 데이터의 분포나 데이터 개수의 영향을 받으므로 데이터의 분포나 데이터의 개수에 따라 R+트리의 성능이 저하될 수 있음
R*-트리
기본적인 구조와 연산은 R-트리와 동일
삽입, 삭제 시 부모 노드의 MBR이 효율적으로 확장될 수 있도록 알고리즘을 개선
R-트리 질의 처리 성능 향상을 위한 고려 사항
- MBR의 면적을 최소화
- MBR 간의 중첩 영역을 최소화
- 둘레 길이 최소화 : 정사각형에 가까운 모양의 MBR이 좋음
- 저장공간 이용률의 최적화 : 트리의 노드 수를 줄이고, 트리의 높이를 낮게 유지한다.

R*-트리의 장점
- R-트리의 기본 구조나 연산을 그대로 유지하고 있으므로 비교적 구현이 간단하다.
- 삽입, 삭제 알고리즘 개선으로 질의 성능이 우수하다.
'File Processing [FP]' 카테고리의 다른 글
| [FP] 09. 다중 키 화일 (2) | 2024.01.23 |
|---|---|
| [FP] 08. 직접 화일 (4) | 2024.01.23 |
| [FP] 07. 인덱스된 순차 화일 (3) | 2024.01.23 |
| [FP] 06. 인덱스 구조 (2) | 2024.01.23 |
| [FP] 05. 화일의 정렬/합병 (1) | 2024.01.22 |



